MATRIKS LANJUTAN
TRANSFORMASI ELEMENTER
Yang dimaksud dengan transformai pada baris atau kolom suatu matriks A adalah sebagai berikut.
- Penukaran tempat baris ke-i dan baris ke-j atau penukaran kolom ke-i dan kolom ke-j dan ditulis Hij(A) untuk transformasi baris dan Kij(A) untuk transformasi kolom.
Contoh :
K13(A) berarti menukar kolom ke-2 matriks A dengan kolom ke-3
2. memperkalikan baris ke-i dengan suatu bilangan skalar h¹0, ditulis Hi(h)(A) dan memperkalikan kolom ke-i dengan skalar k¹0, ditulis Ki(k)(A).
Contoh :
Contoh :
CONTOH SOAL
MATRIKS EKUIVALEN
Dua buah matriks A dan B disebut ekuivalen (A~B) apabila salah satunya dapat diperoleh dari yang lain dengan transformasi-transformasi elementer terhadap baris dan kolom. Kalau transformasi elementer hanya terjadi pada baris saja disebut ELEMENTER BARIS, sedangkan jika transformasi terjadi pada kolom saja disebut ELEMENTER KOLOM.
RANK MATRIKS
Rank matriks adalah jumlah maksimum dari vektor baris atau vektor kolom yang linier independen. Rank matriks ditentukan dari dimensi bujur sangkar dimana vektor baris atau kolomnya tidak bernilai nol. Jika determinan matriks bujur sangkar tidak sama dengan 0 maka rank-nya adalah ordo dari matriks bujur sangkar tersebut.
Rank matriks digunakan untuk menentukan apakah suatu matriks singular atau non-singular. Singular artinya tidak dapat di-invers-kan. Jika determinan matriks adalah 0, maka invers dari matriks tersebut tidak ada, sebab invers matriks berbanding terbalik dengan determinan. Jika determinan 0, maka akan terdapat persamaan 1/0 dalam invers matriks tersebut sehingga invers matriks tidak terdefinisikan.
Determinan Matriks Ordo 2 x 2
Contoh Soal:
Tentukan nilai determinan matriks
Determinan Matriks Ordo 3 x 3

Contoh perhitungan determinan pada matriks ordo 3:
RANK MATRIKS
Rank matriks adalah jumlah maksimum dari vektor baris atau vektor kolom yang linier independen. Rank matriks ditentukan dari dimensi bujur sangkar dimana vektor baris atau kolomnya tidak bernilai nol. Jika determinan matriks bujur sangkar tidak sama dengan 0 maka rank-nya adalah ordo dari matriks bujur sangkar tersebut.
Rank matriks digunakan untuk menentukan apakah suatu matriks singular atau non-singular. Singular artinya tidak dapat di-invers-kan. Jika determinan matriks adalah 0, maka invers dari matriks tersebut tidak ada, sebab invers matriks berbanding terbalik dengan determinan. Jika determinan 0, maka akan terdapat persamaan 1/0 dalam invers matriks tersebut sehingga invers matriks tidak terdefinisikan.
Determinan Matriks
Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau  . Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
. Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
Untuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
Determinan Matriks Ordo 2 x 2
Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
Nilai determinan A disimbolkan dengan  , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
Contoh Soal:
Tentukan nilai determinan matriks
Pembahasan:
Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.
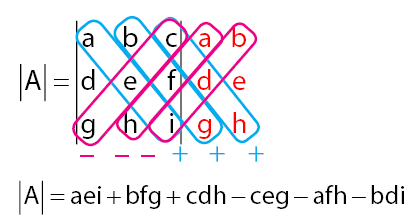
Contoh perhitungan determinan pada matriks ordo 3:
Maka,





Komentar
Posting Komentar